实现Trie前缀树

描述

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True

提示：

1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/implement-trie-prefix-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

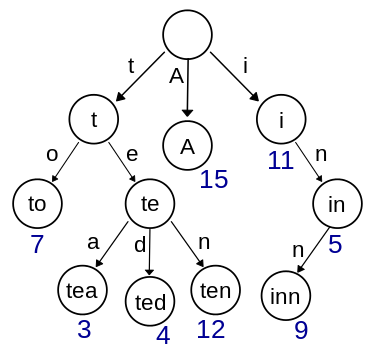
这道题让我们实现一个重要但又有些复杂的数据结构-字典树， 又称前缀树或单词查找树，例如，一个保存了8个键的trie结构，”A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”，如下图所示：

字典树主要有如下三点性质：

1. 根节点不包含字符，除根节点意外每个节点只包含一个字符。

2. 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

3. 每个节点的所有子节点包含的字符串不相同。

C++代码

class Trie {
public:
    /** Initialize your data structure here. */
    Trie() {
        root = new TrieNode(); // 初始化root节点
    }
    
    /** Inserts a word into the trie. */
    void insert(string word) {
        TrieNode* node = root; // 从根节点开始
        for (char c : word) { // 遍历单词的每个字符
            if (!node->children[c - 'a']) { // 如果当前节点没有对应字符的子节点
                node->children[c - 'a'] = new TrieNode(); // 新建一个子节点
            }
            node = node->children[c - 'a']; // 移动到下一个节点
        }
        node->is_end = true; // 单词结束标记
    }
    
    /** Returns if the word is in the trie. */
    bool search(string word) {
        TrieNode* node = root; // 从根节点开始
        for (char c : word) { // 遍历单词的每个字符
            if (!node->children[c - 'a']) { // 如果当前节点没有对应字符的子节点
                return false; // 说明单词不存在
            }
            node = node->children[c - 'a']; // 移动到下一个节点
        }
        return node->is_end; // 判断单词是否结束
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        TrieNode* node = root; // 从根节点开始
        for (char c : prefix) { // 遍历前缀的每个字符
            if (!node->children[c - 'a']) { // 如果当前节点没有对应字符的子节点
                return false; // 说明前缀不存在
            }
            node = node->children[c - 'a']; // 移动到下一个节点
        }
        return true; // 前缀存在
    }

private:
    class TrieNode {
    public:
        bool is_end; // 是否为单词结尾
        TrieNode* children[26]; // 子节点数组，存储a-z的字符
        TrieNode() {
            is_end = false;
            memset(children, NULL, sizeof(children)); // 初始化子节点数组为空
        }
    };
    TrieNode* root; // 根节点
};