下降路径最小和

描述

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

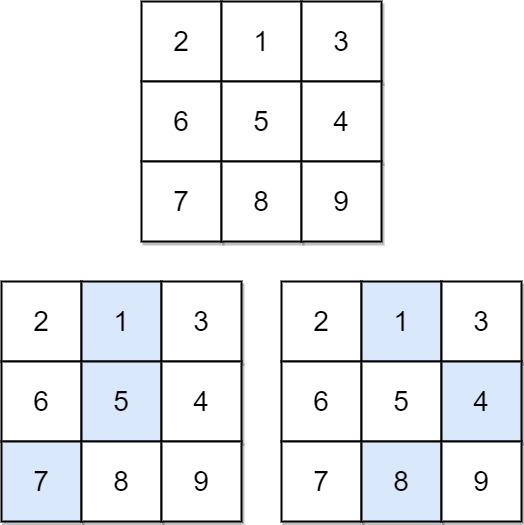
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径
示例 2：

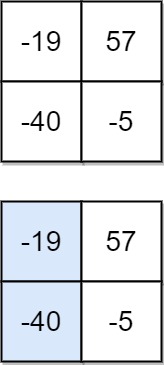
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-falling-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

这道题可以使用动态规划的思想来解决。

我们可以创建一个大小为 n x n 的二维数组 dp，其中 dp[i][j] 表示从第一行到第 i 行，以第 i 行第 j 列为结尾的下降路径的最小和。我们可以使用以下递推公式来计算每个子问题的最小值：

dp[i][j] = A[i][j] + min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1])

其中，A[i][j] 表示当前位置的值，min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) 表示左上角、正上方和右上角三个位置中的最小值。

最后，我们可以在最后一行中找到最小值，并将其作为结果返回。

具体来说，我们首先初始化第一行的最小值为 A[0][i]，然后从第二行开始，对于每个位置 (i, j)，我们可以计算出它的最小值 dp[i][j]，最后在最后一行中找到最小值并返回即可。

C++代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& A) {
        int n = A.size();
        vector<vector<int>> dp(n, vector<int>(n, 0)); // 创建一个大小为 n x n 的二维数组 dp，用于存储每个子问题的最小值
        for (int i = 0; i < n; i++) {
            dp[0][i] = A[0][i]; // 初始化第一行的最小值
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int left = j - 1 >= 0 ? dp[i-1][j-1] : INT_MAX; // 左上角的值
                int up = dp[i-1][j]; // 正上方的值
                int right = j + 1 < n ? dp[i-1][j+1] : INT_MAX; // 右上角的值
                dp[i][j] = A[i][j] + min(left, min(up, right)); // 当前子问题的最小值为当前位置的值加上左上角、正上方和右上角三个位置中的最小值
            }
        }
        int ans = INT_MAX;
        for (int i = 0; i < n; i++) {
            ans = min(ans, dp[n-1][i]); // 最终结果为最后一行的最小值
        }
        return ans;
    }
};