对称二叉树

描述

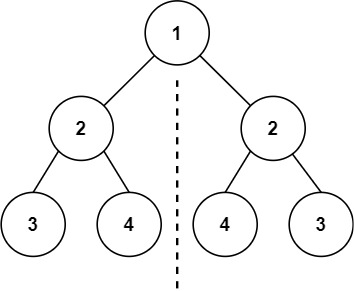
给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true
示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/symmetric-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

C++代码

判断二叉树是否是对称树，比如有两个节点n1, n2，我们需要比较n1的左子节点的值和n2的右子节点的值是否相等，同时还要比较n1的右子节点的值和n2的左子结点的值是否相等，以此类推比较完所有的左右两个节点。我们可以用递归和迭代两种方法来实现，写法不同，但是算法核心都一样。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right){
        // 首先排除空节点的情况
        // 排除了空节点，再排除数值不相同的情况
        if(!left && !right) return true;
        if(left && !right || !left && right || left->val != right->val)
            return false;
        // 此时就是：左右节点都不为空，且数值相同的情况
        // 此时才做递归，做下一层的判断
        return compare(left->left, right->right) && compare(left->right, right->left);
    }

    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        return compare(root->left, root->right);
    }
};

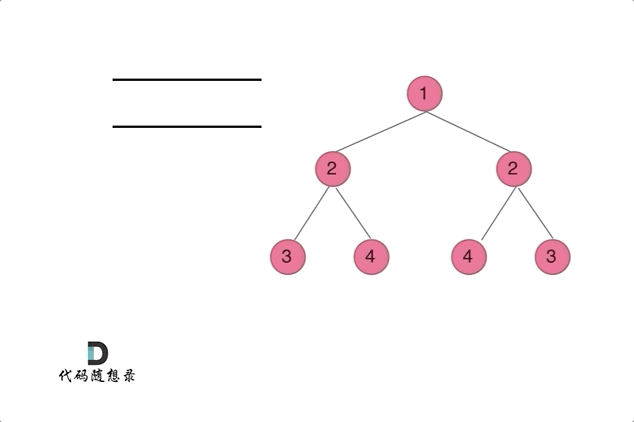
这道题目我们也可以使用迭代法，但要注意，这里的迭代法可不是前中后序的迭代写法，因为本题的本质是判断两个树是否是相互翻转的，其实已经不是所谓二叉树遍历的前中后序的关系了。

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        queue<TreeNode*> q;
        q.push(root->left); // 将左子树头结点加入队列
        q.push(root->right); // 将右子树头结点加入队列
        while(!q.empty()){ // 接下来就要判断这两个树是否相互翻转
            TreeNode* lNode = q.front(); q.pop();
            TreeNode* rNode = q.front(); q.pop();
            if(!lNode && !rNode) // 左节点为空、右节点为空，此时说明是对称的
                continue;
            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if(lNode && !rNode || !lNode && rNode || lNode->val != rNode->val)
                return false;
            q.push(lNode->left);
            q.push(rNode->right);
            q.push(lNode->right);
            q.push(rNode->left);
        }
        return true;
    }
};

Python代码

1、递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def compare(self, left, right) -> bool:
        if not left and not right:
            return True
        if (left and not right) or (not left and right) or (left.val != right.val):
            return False
        return self.compare(left.left, right.right) and self.compare(left.right, right.left) 

    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        return self.compare(root.left, root.right)

2、迭代法

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        q = [root.left, root.right]
        while q:
            lNOde = q.pop(0)
            rNode = q.pop(0)
            if not lNOde and not rNode:
                continue
            if (lNOde and not rNode) or (not lNOde and rNode) or (lNOde.val != rNode.val):
                return False
            q.append(lNOde.left)
            q.append(rNode.right)
            q.append(lNOde.right)
            q.append(rNode.left)
        return True